Math Tools

Solvers

QuantLib provides several types of one-dimensional solvers to solve the roots of single-parameter functions,

$f(x) = 0$

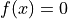
Where 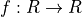$f: R \to R$ is a function over a real number field.

The types of solvers provided by QuantLib are:

Brent
Bisection
Secant
Ridder
Newton (requires member function derivative , calculates derivative)
FalsePosition

The constructors for these solvers are default constructors and do not accept parameters. For example, the construction statement for the Brent solver instance is:

mySolv = Brent()

There are two ways to call the solver’s member function:

mySolv.solve(f, accuracy, guess, step)
mySolv.solve(f, accuracy, guess, xMin, xMax)

f	single parameter function or function object, the return value is a floating point number
accuracy	Floating-point number representing the solution precision used to stop the calculation
guess	a floating-point number, the initial guess for the root
step	Floating point number. In the first calling method, there is no limit to the range of the root. The algorithm needs to search by itself to determine a range. step specifies the step size of the search algorithm.
xMin, xMax	floating point numbers, left and right interval range

ql.Settings.instance().evaluationDate = ql.Date(15,6,2020)
crv = ql.FlatForward(2, ql.TARGET(), 0.05, ql.Actual360())
yts = ql.YieldTermStructureHandle(crv)
engine = ql.DiscountingSwapEngine(yts)

schedule = ql.MakeSchedule(ql.Date(15,9,2020), ql.Date(15,9,2021), ql.Period('6M'))
index = ql.Euribor3M(yts)
floatingLeg = ql.IborLeg([100], schedule, index)

def swapFairRate(rate):
    fixedLeg = ql.FixedRateLeg(schedule, ql.Actual360(), [100.], [rate])
    swap = ql.Swap(fixedLeg, floatingLeg)
    swap.setPricingEngine(engine)
    return swap.NPV()

solver = ql.Brent()

accuracy = 1e-5
guess = 0.0
step = 0.001
solver.solve(swapFairRate, accuracy, guess, step)

Integration

Gaussian Quadrature

Gaussian Quadrature evaluates an integral on a set interval. For example, Gauss-Legendre evaluates the definite integral on the inverval [-1,1]

import numpy as np
import QuantLib as ql

f = lambda x: x**2
g = lambda x: np.exp(x)

quad_ql_legendre = ql.GaussLegendreIntegration(128)
quad_ql_legendre(f), quad_ql_legendre(g)

Scipy also has an implementation that we can compare:

from scipy.integrate import quad
quad(f, -1, 1)[0], quad(g, -1, 1)[0]

Scipy requests an interval [a,b] to operate over. We can achieve the same thing with ql if we scale the input parameters using a wrapper function:

def quad_ql_ab(f, a, b, quad):
    multiplier, ratio = (b+a) / 2, (b-a) / 2
    y = lambda x: f(ratio*x + multiplier)
    return quad(y) * ratio

quad_ql = ql.GaussLegendreIntegration(128)
quad_ql_ab(f, -2, 2, quad_ql), quad_ql_ab(g, -2, 2, quad_ql), quad(f, -2, 2)[0], quad(g, -2, 2)[0]

Other supported quadratures are:

GaussLegendreIntegration,
GaussChebyshevIntegration,
GaussChebyshev2ndIntegration,
GaussLaguerreIntegration,
GaussHermiteIntegration,
GaussJacobiIntegration,
GaussHyperbolicIntegration,
GaussGegenbauerIntegration

The intervals and additional parameters for each quadrature varies (see eg. https://mathworld.wolfram.com/GaussianQuadrature.html)

Interpolation

Interpolation is one of the most commonly used tools in quantitative finance. The standard application scenario is interpolation of yield curves, volatility smile curves, and volatility surfaces. quantlib-python provides the following one- and two-dimensional interpolation methods:

XXXInterpolation(x, y)

x : sequence of floating-point numbers, several discrete arguments
y : sequence of floating-point numbers, the value of the function corresponding to the argument, the same length as x

The interpolation class defines the __call__ method. The usage of an interpolation class object is as follows, as a function

i(x, allowExtrapolation)

x : floating point number, the point to be interpolated
allowExtrapolation : boolean. Setting allowExtrapolation to True means extrapolation is allowed. The default value is False.

1D interpolation method

LinearInterpolation (1-D)
LogLinearInterpolation (1-D)
CubicInterpolation (1-D)
LogCubicInterpolation (1-D)
ForwardFlatInterpolation (1-D)
BackwardFlatInterpolation (1-D)
LogParabolicInterpolation (1-D)

import QuantLib as ql
import numpy as np
import matplotlib.pyplot as plt

X = [1., 2., 3., 4., 5.]
Y = [0.5, 0.6, 0.7, 0.8, 0.9]

methods = {
    'Linear Interpolation': ql.LinearInterpolation(X, Y),
    'LogLinearInterpolation': ql.LogLinearInterpolation(X, Y),
    'CubicNaturalSpline': ql.CubicNaturalSpline(X, Y),
    'LogCubicNaturalSpline': ql.LogCubicNaturalSpline(X, Y),
    'ForwardFlatInterpolation': ql.ForwardFlatInterpolation(X, Y),
    'BackwardFlatInterpolation': ql.BackwardFlatInterpolation(X, Y),
    'LogParabolic': ql.LogParabolic(X, Y)
}

xx = np.linspace(1, 10)
fig = plt.figure(figsize=(15,4))
plt.scatter(X, Y, label='Original Data')
for name, i in methods.items():
    yy = [i(x, allowExtrapolation=True) for x in xx]
    plt.plot(xx, yy, label=name);
plt.legend();

2D Interpolation Methods

BilinearInterpolation (2-D)
BicubicSpline (2-D)

import pandas as pd
X = [1., 2., 3., 4., 5.]
Y = [0.6, 0.7, 0.8, 0.9]
Z = [[(x-3)**2 + y for x in X] for y in Y]
df = pd.DataFrame(Z, columns=X, index=Y)

i = ql.BilinearInterpolation(X, Y, Z)

XX = np.linspace(0, 5, 9)
YY = np.linspace(0.55, 1.0, 10)

extrapolated = pd.DataFrame(
    [[i(x,y, True) for x in XX] for y in YY],
    columns=XX,
    index=YY)


from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from matplotlib import cm

fig = plt.figure()
ax = fig.gca(projection='3d')
ax.set_title("Surface Interpolation")

Xs, Ys = np.meshgrid(XX, YY)
surf = ax.plot_surface(
    Xs, Ys, extrapolated, rstride=1, cstride=1, cmap=cm.coolwarm
)
fig.colorbar(surf, shrink=0.5, aspect=5);

Optimization

Random Number Generators

Quantlib-Python provides the following three uniformly distributed (pseudo) random number generators:

ql.KnuthUniformRng, Knuth algorithm
ql.LecuyerUniformRng, L’Ecuyer algorithm
ql.MersenneTwisterUniformRng, the famous Mersenne-Twister algorithm

The constructor of the random number generator,

RandomNumberGenerator(seed)

where seed is an integer, with a default value of 0, used as a seed to initialize the corresponding deterministic sequence

Member functions of the random number generator:

next() : Returns a SampleNumber object as the result of the simulation.

r = rng.next()
v = r.value(r)

The user obtains a series of random numbers by repeatedly calling the member function next(). It should be noted that the type of r is SampleNumber , and the corresponding floating-point number needs to be called by calling value() .

The most common distribution in random simulations is the normal distribution. There are four types of normally distributed random number generators provided by quantlib-python:

CentralLimit[X]GaussianRng
BoxMuller[X]GaussianRng
MoroInvCumulative[X]GaussianRng
InvCumulative[X]GaussianRng

Where [X] refers to a uniform random number generator.

Specifically, there are 12 types of 4 types of generators:

CentralLimitLecuyerGaussianRng
CentralLimitKnuthGaussianRng
CentralLimitMersenneTwisterGaussianRng
BoxMullerLecuyerGaussianRng
BoxMullerKnuthGaussianRng
BoxMullerMersenneTwisterGaussianRng
MoroInvCumulativeLecuyerGaussianRng
MoroInvCumulativeKnuthGaussianRng
MoroInvCumulativeMersenneTwisterGaussianRng
InvCumulativeLecuyerGaussianRng
InvCumulativeKnuthGaussianRng
InvCumulativeMersenneTwisterGaussianRng

Constructor of random number generator:

GaussianRandomNumberGenerator(RandomNumberGenerator)

BoxMullerMersenneTwisterGaussianRng distributed random number generators accept a corresponding uniformly distributed random number generator as the source.

Taking BoxMullerMersenneTwisterGaussianRng as an example, you need to configure a MersenneTwisterUniformRng object as the source of random numbers, and use the classic Box-Muller algorithm to obtain normal distributed random numbers.

seed = 12324
unifMt = ql.MersenneTwisterUniformRng(seed)
bmGauss = ql.BoxMullerMersenneTwisterGaussianRng(unifMt)

for i in range(5):
    print(bmGauss.next().value())

Compared with the “pseudo” random numbers described earlier, another important type of random numbers in random simulations becomes “quasi” random numbers, also known as low-bias sequences. Because of better convergence, quasi-random numbers are often used in the simulation of high-dimensional random variables. There are two types of quasi-random numbers provided by quantlib-python,

HaltonRsg : Halton sequence
SobolRsg : Sobol sequence

HaltonRsg

HaltonRsg(dimensionality, seed, randomStart, randomShift)

where,

dimensionality : integer, set the dimension;
seed : an integer, with a default value of 0, used as a seed to initialize the corresponding deterministic sequence;
randomStart : boolean, the default is True , whether to start randomly;
randomShift : Boolean, default is False , whether to shift randomly.

Member function of HaltonRsg,

nextSequence() : returns a SampleRealVector object as the result of the simulation;
lastSequence() : returns a SampleRealVector object as the result of the previous simulation;
dimension() : Returns the dimension.

SobolRsg

SobolRsg(dimensionality, seed, directionIntegers=Jaeckel)

where,

dimensionality : integer, set the dimension;
seed : an integer, with a default value of 0, used as a seed to initialize the corresponding deterministic sequence;
directionIntegers : a built-in variable of quantlib-python. The default value is SobolRsg.Jaeckel , which is used to initialize Sobol sequences.

Member functions of SobolRsg,

nextSequence() : returns a SampleRealVector object as the result of the simulation;
lastSequence() : returns a SampleRealVector object as the result of the previous simulation;
dimension() : Returns the dimension.
skipTo(n) : n is an integer, skip to the nth dimension of the sampling result;
nextInt32Sequence() : Returns an IntVector object.

Path Generators

QuantLib provides several wrapper functions to produce sample paths from a given stochastic process

GaussianMultiPathGenerator

Generate paths from an arbitrary stochastic process using pseudorandom numbers

ql.GaussianMultiPathGenerator(stochasticProcess, times, sequenceGenerator, brownianBridge=False)

timestep, length, numPaths = 24, 2, 2**15

today = ql.Date().todaysDate()
riskFreeTS = ql.YieldTermStructureHandle(ql.FlatForward(today, 0.05, ql.Actual365Fixed()))
dividendTS = ql.YieldTermStructureHandle(ql.FlatForward(today, 0.01, ql.Actual365Fixed()))
initialValue = ql.QuoteHandle(ql.SimpleQuote(100))

v0, kappa, theta, rho, sigma = 0.005, 0.8, 0.008, 0.2, 0.1
hestonProcess = ql.HestonProcess(riskFreeTS, dividendTS, initialValue, v0, kappa, theta, sigma, rho)

times = ql.TimeGrid(length, timestep)
dimension = hestonProcess.factors()

rng = ql.UniformRandomSequenceGenerator(dimension * timestep, ql.UniformRandomGenerator())
sequenceGenerator = ql.GaussianRandomSequenceGenerator(rng)
pathGenerator = ql.GaussianMultiPathGenerator(hestonProcess, list(times), sequenceGenerator, False)

# paths[0] will contain spot paths, paths[1] will contain vol paths
paths = [[] for i in range(dimension)]
for i in range(numPaths):
    samplePath = pathGenerator.next()
    values = samplePath.value()
    spot = values[0]

    for j in range(dimension):
        paths[j].append([x for x in values[j]])

GaussianSobolMultiPathGenerator

Generate paths from an arbitrary stochastic process using low discrepency numbers

ql.GaussianSobolMultiPathGenerator(stochasticProcess, times, sequenceGenerator, brownianBridge=False)

timestep, length, numPaths = 24, 2, 2**15

today = ql.Date().todaysDate()
riskFreeTS = ql.YieldTermStructureHandle(ql.FlatForward(today, 0.05, ql.Actual365Fixed()))
dividendTS = ql.YieldTermStructureHandle(ql.FlatForward(today, 0.01, ql.Actual365Fixed()))
initialValue = ql.QuoteHandle(ql.SimpleQuote(100))

v0, kappa, theta, rho, sigma = 0.005, 0.8, 0.008, 0.2, 0.1
hestonProcess = ql.HestonProcess(riskFreeTS, dividendTS, initialValue, v0, kappa, theta, sigma, rho)

times = ql.TimeGrid(length, timestep)
dimension = hestonProcess.factors()

rng = ql.UniformLowDiscrepancySequenceGenerator(dimension * timestep)
sequenceGenerator = ql.GaussianLowDiscrepancySequenceGenerator(rng)
pathGenerator = ql.GaussianSobolMultiPathGenerator(hestonProcess, list(times), sequenceGenerator, False)

# paths[0] will contain spot paths, paths[1] will contain vol paths
paths = [[] for i in range(dimension)]
for i in range(numPaths):
    samplePath = pathGenerator.next()
    values = samplePath.value()
    spot = values[0]

    for j in range(dimension):
        paths[j].append([x for x in values[j]])

Statistics

Convention Calculators

BlackDeltaCalculator

A calculator class to calculate the relevant strike for FX-style delta-maturity-vol quotes (see Reiswich D., Wystup U., 2010. A Guide to FX Options Quoting Conventions)

ql.BlackDeltaCalculator(optionType, deltaType, spot, domesticDcf, foreignDcf, volRootT)

import numpy as np

today = ql.Date().todaysDate()
dayCounter = ql.Actual365Fixed()
spot = 100
rd, rf = 0.02, 0.05

ratesTs = ql.YieldTermStructureHandle(ql.FlatForward(today, rd, dayCounter))
dividendTs = ql.YieldTermStructureHandle(ql.FlatForward(today, rf, dayCounter))

# Details about the delta quote
optionType = ql.Option.Put
vol = 0.07
maturity = 1.0
deltaType = ql.DeltaVolQuote.Fwd      # Also supports: Spot, PaSpot, PaFwd

# Set up the calculator
localDcf, foreignDcf = ratesTs.discount(maturity), dividendTs.discount(maturity)
stdDev = np.sqrt(maturity) * vol
calc = ql.BlackDeltaCalculator(optionType, deltaType, spot, localDcf, foreignDcf, stdDev)

To calculate the strike for a given call/put delta (negative for put delta)

delta = -0.3
calc.strikeFromDelta(delta)

Or if this is an ATM quote, specify the ATM convention

atmType = ql.DeltaVolQuote.AtmFwd     # Also supports: AtmSpot, AtmDeltaNeutral, AtmVegaMax, AtmGammaMax, AtmPutCall50
calc.atmStrike(atmType)